Quels sont les outils utilisés par les économistes ? Le Professeur Moez Ouni vous propose de les découvrir dans ce nouvel article.
1. La modélisation
Comme les différentes sciences, la science économique essaie d’adopter une démarche pour expliquer les phénomènes économiques. Une facette de la démarche consiste en l’utilisation de la modélisation.
La modélisation signifie une schématisation représentative de la réalité économique. Il faut dire que la réalité est tellement complexe qu’aucun modèle ne peut la cerner. Cela implique que n’importe quel modèle se base sur des hypothèses, choisit une partie de la réalité afin de l’expliquer.
Cette explication passe bien évidemment à travers la réduction de la réalité à quelques relations entre différentes variables. Il s'ensuit qu'un modèle économique est « un système abstrait dont la fonction est de représenter la réalité de façon très simplifiée, mais formalisée, ou de permettre l'étude d'un phénomène réel. » (Dictionnaire d'économie et sciences sociales, Nathan Paris, 1993).
Un modèle est par définition réducteur. Nous rencontrons plusieurs modèles dans les différentes branches de l’économie. Par exemple : le modèle de croissance économique, le modèle d’équilibre général, le modèle d’offre et de demande sur un marché concurrentiel, le modèle de Ricardo en commerce international, etc.
Les modèles sont utiles pour différentes raisons :
- La modélisation permet d’identifier les éléments (variables et phénomènes) d’un processus économique.
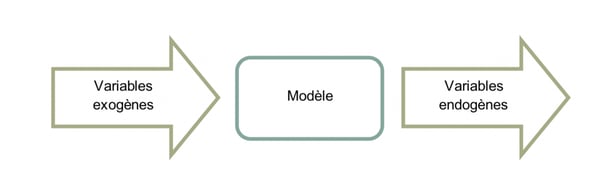
- La modélisation permet d’expliquer (même partiellement) l’évolution et la tendance d’une variable (un phénomène) par l’influence d’autres variables (phénomènes). Donc, la modélisation permet d’identifier les relations (de cause à effet par exemple) existantes entre les différentes variables. Nous parlons de variables expliquées (endogènes) et de variables explicatives (exogènes).
- La modélisation permet de franchir le pas pour utiliser les statistiques et établir les relations empiriquement et non pas uniquement théoriquement.
- La modélisation permet la simulation économique. Il s’agit d’une manière de reproduction pour observer le fonctionnement de phénomènes économique à l’aide d’un modèle. C’est reproduire artificiellement un système (vu l’impossibilité de reproduire la réalité économique en laboratoire) pour expérimenter les comportements possibles de ses éléments.
- La modélisation aide à la prévision. Cette dernière vise à estimer, par le biais de différentes méthodes, l’évolution future des différentes variables économiques telles que le PIB (le produit intérieur brut), le chômage, l’inflation, les exportations, les finances publiques, la croissance économique, le taux de change, etc. Pour parvenir à établir des prévisions à court terme, les économistes utilisent des modèles économétriques, la méthode Delphi, l’expérience, etc.
- La modélisation est un appui à l’action de politique économique. Lorsque les décideurs possèdent les résultats d’une modélisation économique, cela peut les aider à prendre des décisions en connaissance de cause. Mais, il faut prendre toutes les précautions nécessaires lors de l’interprétation des résultats de la modélisation, car tout modèle est réducteur et ne peut en aucun cas cerner la réalité économique dans sa complexité. Cependant, la modélisation reste d’une grande utilité chez les économistes dans leurs démarches scientifiques.
a. Exemple n° 1 de modélisation : la concurrence pure et parfaite
Offre et demande sur un marché de concurrence pure et parfaite.
Les économistes ont eu l’habitude de modéliser le fonctionnement d’un marché quelconque par le jeu de l’offre et la demande. Ils utilisent un modèle de référence théorique qui est « le marché en concurrence pure et parfaite ». Ce marché se caractérise par les hypothèses suivantes :
- L’atomicité de l’offre et de la demande (plusieurs offreurs et plusieurs demandeurs) ; cela veut dire que les consommateurs et les producteurs pris individuellement n’ont pas d’influence sur le prix (qui est considéré comme exogène) ;
- Les consommateurs et les producteurs doivent agir individuellement (pas de collusion);
- Le marché est libre (libre entrée et sortie du marché);
- Le marché est transparent (information parfaite) : les participants ont une connaissance parfaite des prix proposés sur le marché et des caractéristiques des produits ;
- Le produit est homogène ;
- Mobilité parfaite des facteurs de production (travail et capital).
Si ces conditions sont remplies, le mécanisme de fixation des prix est la confrontation de l’offre et de la demande (loi de l’offre et de la demande). Nous parlons dans ce cas d’équilibre sur le marché de concurrence pure et parfaite. Cet équilibre est obtenu par la confrontation de l’offre et de la demande sur le marché. On aboutit à une quantité et à un prix dit d’équilibre.
Graphiquement, nous présentons l’équilibre du marché comme suit.
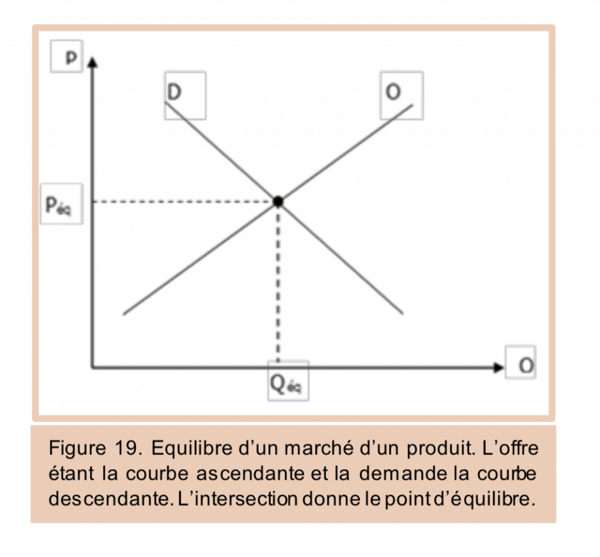
La droite D représente la demande des consommateurs (demandeurs) et la droite O représente la courbe d’offre des producteurs (offreurs). L’équilibre sur ce marché est atteint lorsque les quantités offertes et demandées sont égales. Cette situation permet de déterminer un prix d’équilibre "Péq" sur l’axe des ordonnées et une quantité d’équilibre "Qéq" sur l’axe des abscisses.
b) Exemple n° 2 de modélisation : le circuit économique
L'économie est constituée de millions de personnes engagées dans de nombreuses activités d'achat, de vente, de travail, de fabrication, et ainsi de suite. Pour comprendre comment l'économie fonctionne, nous devons trouver un moyen pour simplifier notre réflexion sur toutes ces activités. En d'autres termes, nous avons besoin d'un modèle qui explique, en termes généraux, comment l'économie est organisée et comment les participants à l’activité économique interagissent les uns avec les autres.
Pour y parvenir, les économistes utilisent une manière simple pour représenter l’organisation économique. Il s’agit du circuit économique. On le définit comme un schéma synthétique montrant les relations économiques entre les différents agents dans une économie.
Pour des raisons de clarté et de simplicité, nous présentons des circuits avec 2 et 3 agents économiques (ménages, entreprises, Etat). Nous pouvons trouver dans la littérature des circuits plus développés et plus complexes.
Les opérations économiques sont représentées par des flux : mouvements de biens, de services ou de monnaie. Ce sont le résultat des échanges entre des agents à l’occasion d’une opération et pendant une période de temps donnée. Il existe deux types de flux :
- Les flux réels ou physiques : biens et services échangés.
- Les flux financiers ou monétaires : monnaie échangée.
Il faut se rappeler que les différentes opérations économiques se déroulent sur un marché : marché des biens et services, marché des facteurs de production (capital, travail, etc.). En contrepartie de toute opération impliquant un échange de bien ou de prestation de service, il y a l’équivalent monétaire. Voici deux circuits économiques d’une économie formée par 2 et 3 agents.
Circuit économique simple avec deux agents : ménages et entreprises
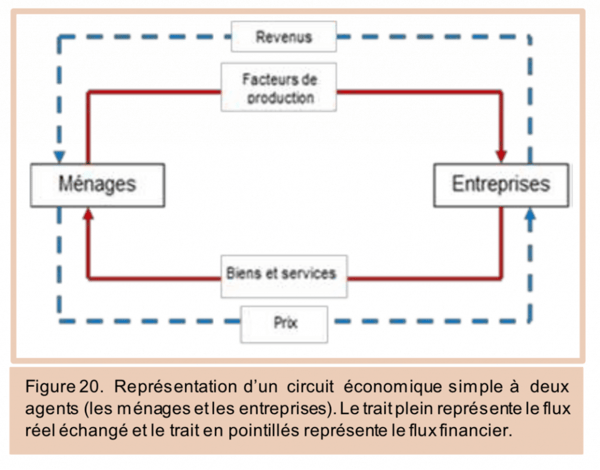
Pour lire correctement ce schéma, les traits pleins représentent les flux dits réels (de biens et services) et les traits en pointillés représentent les flux monétaires (flux d’argent).
Circuit économique avec 3 agents : ménages, entreprises et Etat
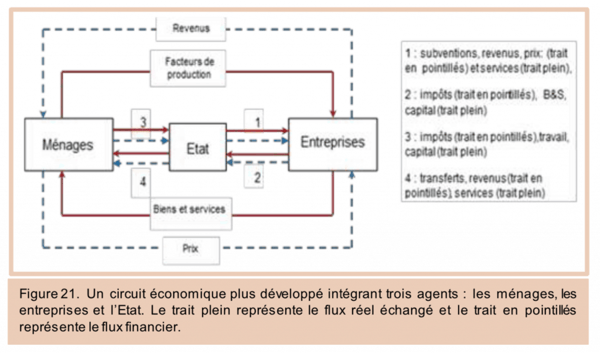
Nous pouvons aussi inscrire sur le circuit les variables ou les montants représentant les différentes relations entre les agents. Le circuit suivant, tiré d’une publication de l’OFS (Office fédéral de la statistique), montre bien ce cas.
Remarque
Il faut distinguer entre flux et stock. En économie, le terme stock a deux sens :
- Les quantités des biens stockés au sein d’une entreprise par exemple. On y trouve les matières premières, les produits semi-finis et les produits finis.
- Dans son deuxième sens, il signifie l’état d’une variable qui s’oppose à la notion de flux. Par exemple, le stock de capital d’une économie. Dans ce sens, il existe une relation fondamentale entre le stock et le flux :
Stocks en t = stocks en t-1 + flux entrants – flux sortants
et
Flux net = flux entrants – flux sortants
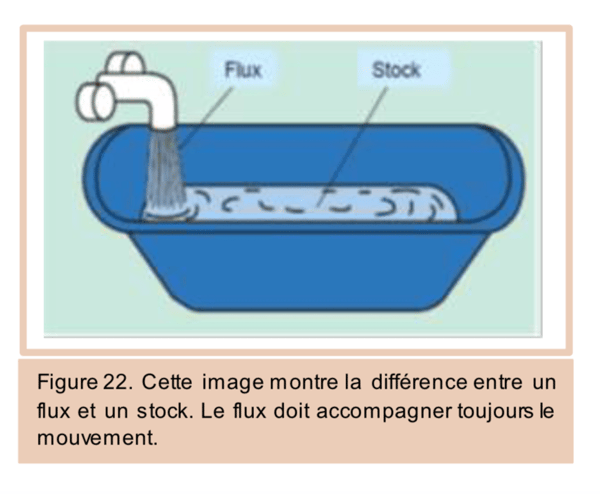
Schématiquement, pour distinguer entre flux et stock, on fait appel à la parabole de la baignoire : l’eau qui coule du robinet représente le flux et l’eau se trouvant dans la baignoire représente le stock à un moment donné. Pour mesurer le flux, il faut fixer deux points : un point de départ et un point d’arrivée.
2. Les mathématiques
L’utilisation des mathématiques en sciences économiques est courante. C’est à partir du XVIIIe siècle qu’on a commencé à formaliser les sciences économiques par le recours à l’utilisation des fonctions mathématiques pour étudier le comportement et les relations des variables économiques, par exemple la fonction de demande. Par la suite, les économistes ont eu de plus en plus recours aux outils mathématiques dans leur démarche, en particulier, à partir de la révolution marginaliste et les années qui ont suivi.
Les outils les plus couramment utilisés par les économistes à ce stade des études sont : les fonctions, les graphiques, les dérivées, le calcul différentiel, l’optimisation sous ou sans contrainte et le calcul matriciel. Tous ces outils font partie d’un cours de mathématiques pour économiste (y compris dans notre université). Les exemples dans ce domaine ne manquent pas.
3. La courbe de Lorenz
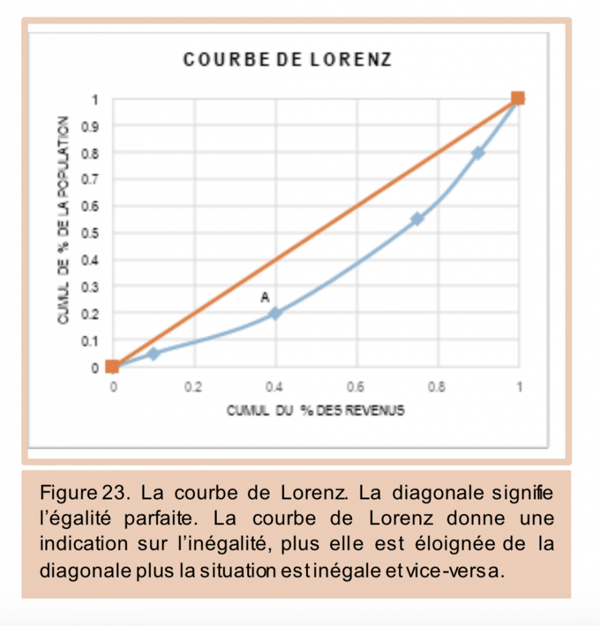
La courbe de Lorenz est une représentation graphique de la fonction de répartition d’une variable quelconque. Elle est utilisée par les économistes, notamment, pour mesurer les inégalités de distribution des richesses (comme les revenus, la fortune personnelle, etc.). Elle permet de représenter une fonction de répartition reliant des proportions de la population aux parts des richesses détenues par ces proportions.
D’une autre manière, elle permet de relier les parts X de la population aux parts Y de la richesse détenues par la population. Elle est représentée toujours dans le plan (0,0) et (1,1) et se situe en dessous de la diagonale (qui désigne la situation d’égalité parfaite). Plus la courbe est proche de cette diagonale, plus la répartition est égalitaire.
En revanche, plus elle est éloignée de cette diagonale, plus la distribution est inégalitaire. Les cas extrêmes sont 1) la courbe de Lorenz se confond avec la diagonale (parfaite égalité), et 2) la courbe de Lorenz se confond avec l’axe horizontal et au point 1 elle se confond avec l’axe vertical (parfaite inégalité). Un point quelconque (comme le point A) de la courbe s’interprète de la manière suivante : 40% des revenus sont détenus par 20% de la population totale.
Indice de Gini
L'indice de Gini est un coefficient qui synthétise l’inégalité de la distribution de la richesse au sein d’une population par exemple. Il prend des valeurs entre 0 et 1 (ou 0 et 100). Plus l’indice est proche de 0, plus la distribution est égalitaire et inversement. Entre 0 et 1 (ou 0 et 100), l'inégalité est d'autant plus forte que l'indice de Gini est élevé. Il se calcule en général à partir de la courbe de Lorenz. Il est égal au rapport entre la surface limitée par la diagonale et la courbe de Lorenz et toute la surface en dessous de la diagonale (le triangle).
Tableau : Indice de Gini publié par la Banque mondiale pour certains pays
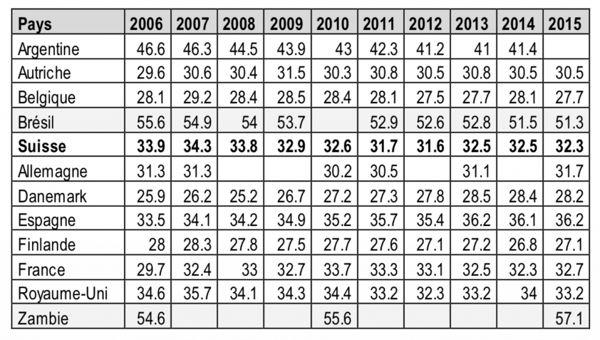
Source : BM, 2018.
On remarque que certains pays comme le Brésil et la Zambie sont moins égalitaires que des pays comme la Suisse ou le Danemark par exemple.
Une image vaut mille mots. Avec ce dicton, les économistes font beaucoup appel à un outil très simple mais très important : les graphiques. Avec quelques lignes et quelques points, beaucoup de choses peuvent être présentées et véhiculées. Dans cette section, nous présentons quelques types de graphiques qui sont fréquemment utilisés par les économistes.
4.1. Le graphique (ou diagramme) à une variable
Ce type de graphique est utilisé pour donner une idée sur la distribution d’une variable et/ou son évolution dans le temps. Nous trouvons les graphes suivants :
- Graphique de nuage de points (lorsqu’il s’agit de valeurs discrètes) ;
- Graphique présentant une courbe ou une tendance (droite ou une forme quelconque) ;
- Graphique circulaire ou camembert (Pie Chart en anglais) ;
- Graphique présentant un histogramme.
Pour présenter ces différents graphes, nous donnons un exemple chiffré. Il s’agit de statistiques du PIB et de la consommation finale des ménages de la Suisse entre 1998 et 2017.
Tableau : Revenu et consommation des ménages en Suisse
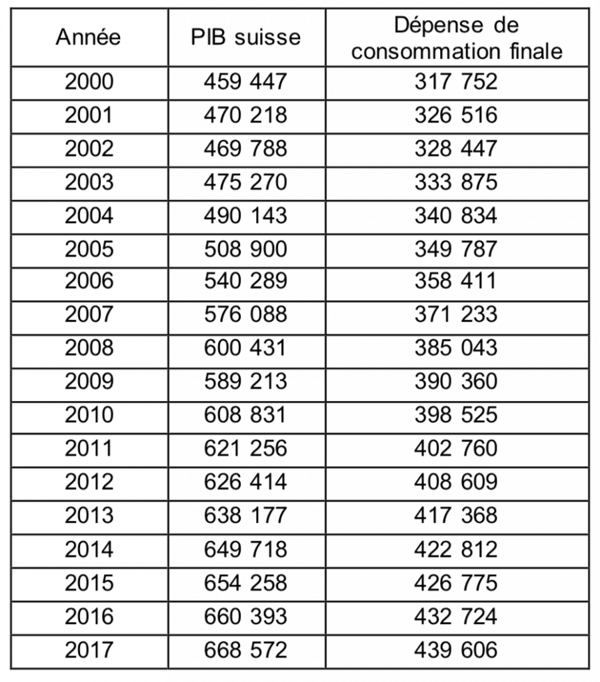
Source : OFS, 2018.
a) Graphique avec une variable
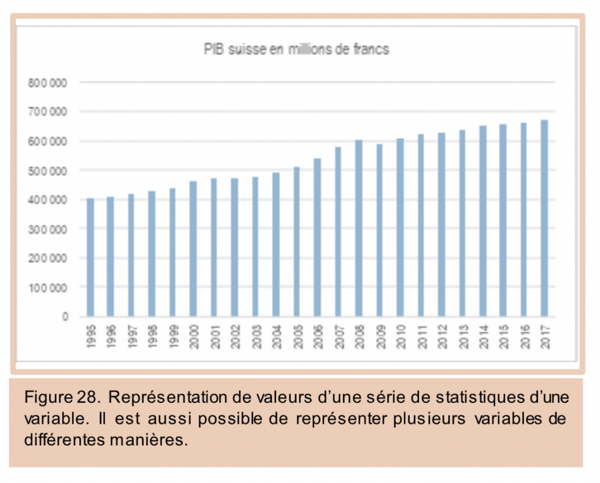
Nous présentons ici à titre illustratif la courbe de trajectoire (l’évolution) du PIB suisse à travers le temps (entre 1990 et 2017).
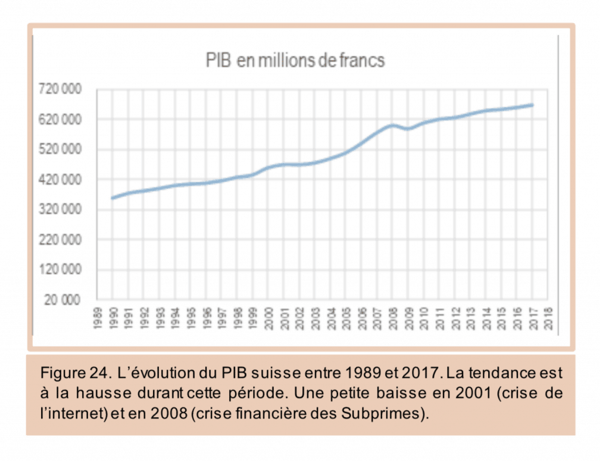
Nous pouvons même mettre plusieurs courbes ensemble pour autant qu’elles ont une même échelle. De nouveau, nous recourons aux chiffres du tableau ci-dessus et allons représenter les deux séries de la Suisse : PIB et consommation des ménages.
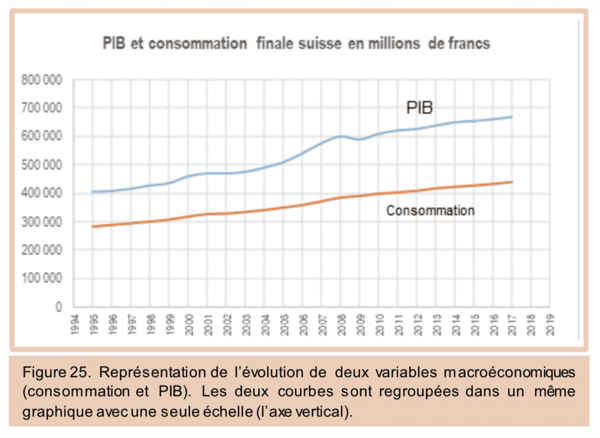
b) Graphique camembert
Un camembert se présente comme un disque. Il est découpé par des rayons, c'est-à-dire des segments partant du centre vers la périphérie. Plusieurs zones apparaissent, chacune délimitée par deux rayons et un arc de cercle : elles sont appelées secteurs angulaires. En général, on remplit chaque secteur angulaire d'une couleur différente, ou d'une teinte de gris différente. Chaque secteur angulaire est associé à une valeur des données. Une légende explique à quelle couleur est associée quelle donnée. La représentation de nombres négatifs est impossible avec ce type de diagramme.
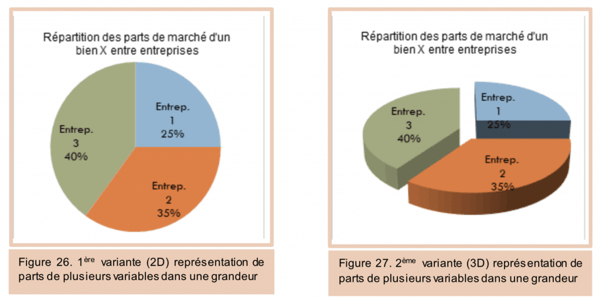
c) Graphique avec une variable : Histogramme
L’histogramme est une représentation graphique d’une ou de plusieurs variables (ayant le même axe) sous forme de bâtons, barres, ou en tuyaux. L'histogramme est composé de colonnes de hauteurs variables mises l’une à côté de l’autre. L'ordonnée (axe Y ou vertical) reçoit les valeurs et l'abscisse (axe X ou horizontal) les catégories.
Graphiquement, si nous prenons les valeurs de la série du PIB suisse, nous obtenons le résultat suivant :
4.2. Le graphique (ou diagramme) à deux variables
Le plus simple des graphiques à plusieurs variables est celui qui utilise deux variables. Le but de ce graphique est la mise en relation de deux variables : une sur l’axe des ordonnées (ou des Y ou l’axe vertical) et l’autre sur l’axe des abscisses (ou des X ou l’axe horizontal). Mathématiquement parlant, la relation est du type : Y = f(X). Y est une fonction de X. La représentation de cette fonction peut donner lieu à différents types de graphiques :
- Graphique de nuage de points (lorsqu’il s’agit de valeurs discrètes).
- Graphique présentant une courbe (droite ou une forme quelconque).
Nous nous limitons à ces formes. Pour illustrer ce type de graphe, nous nous basons sur des statistiques réelles tirées de la publication de l’Office fédéral de la statistique (OFS) concernant l’économie nationale de la période 1990 jusqu’à 2009.
Nous savons que la relation entre consommation et revenu est une relation positive, plus le revenu augmente, plus la consommation augmente.
a) Graphique de nuage de points à deux variables
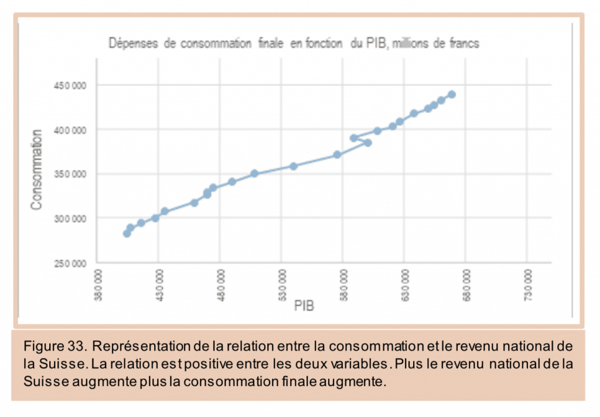
Si nous mettons en relation ces deux grandeurs (consommation des ménages en fonction du revenu national) et choisissons la forme de nuage de points, nous obtenons le graphique ci-dessous. Il faut rappeler que le nuage de point peut nous donner une idée première sur l’existence ou l’absence d’une quelconque relation entre les variables en présence. Si nous tirons une droite passant par le milieu du nuage des points, nous pouvons avoir trois cas possibles :
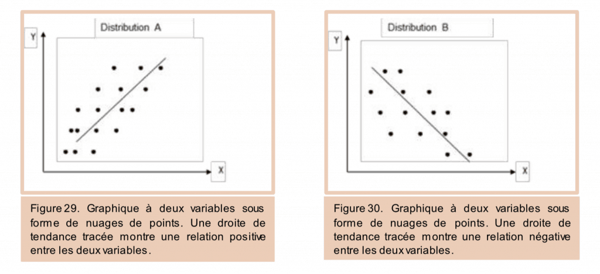
- La droite passant par le centre du nuage est de pente positive (croissante), nous concluons à une relation positive (distribution A) ;
- La droite passant par le centre du nuage est de pente négative (décroissante), nous concluons à une relation négative (distribution B) ;
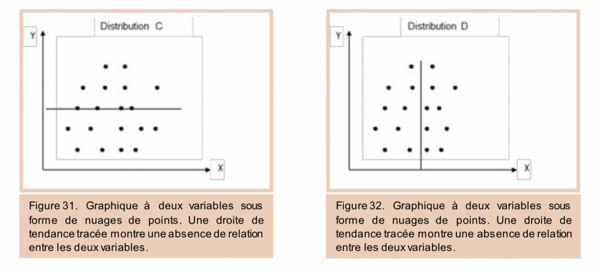
- La droite passant par le centre du nuage est horizontale (de pente nulle), distribution C, nous concluons à une absence de relation ;
- La droite passant par le centre du nuage est verticale (de pente infinie), distribution D, nous concluons à une absence de relation.
Si nous reprenons les données de la Suisse de la consommation et du revenu, nous pouvons représenter leur relation (consommation en fonction du revenu) dans le graphique suivant. Chaque point correspond à un couple de valeurs (consommation, revenu) pour une année donnée. La période s’étend de 1990 à 2017. Le nuage de points montre que la relation entre la consommation et le revenu est positive : plus le revenu augmente, plus la consommation augmente.
b) Graphique présentant une courbe (droite ou une forme quelconque)
Le deuxième type de graphe utilisé est un graphique représentant une courbe continue dans un plan XY. La continuité signifie qu’à tout point de l’abscisse de l’axe des abscisses correspond une image (valeur de Y) et une seule. Avec ce type de graphique nous pouvons nous poser la question non seulement sur la nature de la relation mais aussi sur l’impact de la variation d’une variable sur l’autre. Autrement dit, si X varie de ∆X (= quantité quelconque) quel sera la variation de Y, c’est-à-dire ∆Y, tous les autres facteurs susceptibles d’influencer Y sont considérés constants. Nous parlons dans ce cas de la pente de la courbe qui n’est autre que le rapport des variations des deux variables lorsqu’elles sont infinitésimales (très petites variations) :
la pente d′une courbe = ∆Y / ∆X
Courbe particulière : la droite
Pour illustrer ce concept, nous utilisons une courbe simple : une droite. La pente de la droite est par définition constante. Par exemple, Y = a X + b. La droite qui sera représentée graphiquement a pour pente le paramètre a et l’ordonnée à l’origine (lorsque X = 0) le paramètre b.
la pente d′une courbe droite = ∆Y / ∆X = a
Le paramètre a peut prendre différentes valeurs (négative, positive ou nulle). Mathématiquement parlant, la pente correspond à la dérivée première d’une fonction. Dans le cas d’une droite, la pente est la même en tout point. Cependant, elle est en général variable suivant la position du point dans la courbe.
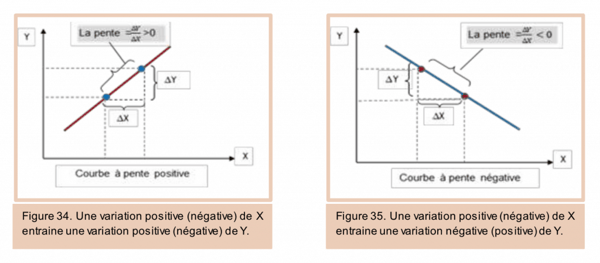
Cas particuliers de droite
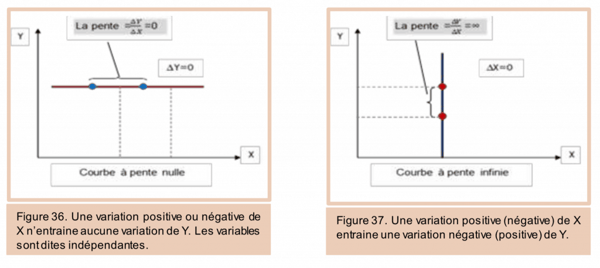
Courbe quelconque
En science économique, nous utilisons les courbes de différentes formes et allures en plus des droites. Le calcul de la pente n’est pas le même que dans le cas d’une droite. Dans le cas d’une courbe quelconque, la pente varie selon les points de la courbe. Pour y parvenir, il faut tracer la tangente au point désigné (par exemple le point A dans le graphique suivant). Après, nous choisissons deux points sur la droite tangente (C et D) qui nous permettent de calculer la pente au point A. De nouveau, la pente de la courbe au point A est égale à la dérivée première calculée en ce point.
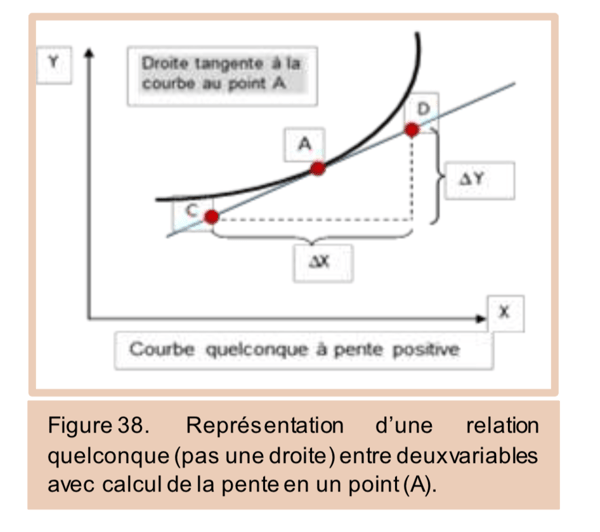
L’utilisation des dérivées en science économique a un sens bien précis. L’analyse à la marge ou marginale fait appel à la notion de dérivée car cela signifie que nous travaillons avec des variations très petites (infinitésimales).
Autres représentations graphiques
La représentation des relations entre variables économiques ou de simples variables ne se limitent pas aux graphiques présentés jusqu’à maintenant. Les économistes utilisent d’autres formes de représentation plus compliquées. Par exemple, les graphiques à double échelle, graphiques boursiers, graphiques radars, etc.
Une nouvelle formation en économie en ligne vous intéresse ? Contactez-nous dès maintenant afin d’être informé(e) de sa mise en ligne !
5. Les statistiques
A partir du XVIIIe siècle, les économistes ont commencé à se servir des statistiques comme outil d’analyse des phénomènes économiques. Différents auteurs ont contribué au développement des mathématiques et des probabilités qui a permis une avancée importante dans l’utilisation de la statistique. L’utilisation de la statistique dans les sciences économiques facilite les tâches suivantes :
La description des données
Décrire les données peut se faire de plusieurs manières sous forme de tableaux, de graphiques, de cartes ou sous d’autres formes. Dans la description des données, nous trouvons généralement les indicateurs synthétiques :
- Valeurs centrales : la moyenne, le mode, la médiane, les quartiles.
- De dispersion : variance, écart-type, étendue, valeurs maximale et minimale, Kurtosis (coefficient d’aplatissement de la distribution), Skewness (coefficient d’asymétrie de la distribution).
A titre d’exemple, en utilisant Excel, nous obtenons les informations suivantes sur la série PIB suisse.
Tableau : PIB Suisse de 1998 à 2017
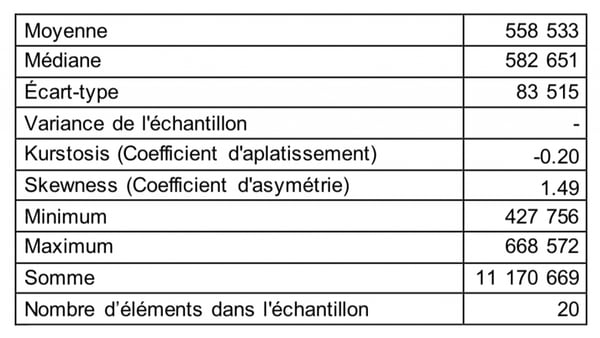
L’inférence statistique
Le développement des probabilités a donné un appui au développement de la statistique inférentielle. Le but de la manœuvre est qu’à partir d’un échantillon aléatoire d’une population, nous essayons de comprendre les caractéristiques de cet échantillon et de généraliser ce résultat à la population, avec bien évidemment une marge d’erreur. Les statisticiens agissent de la sorte car ils ne peuvent pas traiter directement avec la population. Comme l’échantillon est aléatoire, nous faisons appel aux probabilités pour calculer la marge d’erreur. Une grande partie de l’inférence statistique s’appuie sur les tests statistiques (test de Student, de Fisher, de Chi 2, ...). La statistique étudie certaines caractéristiques : caractères ou variables d'un ensemble fini appelé échantillon (tiré aléatoirement d’une population). Les éléments de l’échantillon étudié (ou de la population) sont appelés individus.
L’analyse des séries statistiques
Les économistes utilisent deux types de données :
- Les séries transversales (Cross section en anglais) : ce sont des données de plusieurs individus pris en même temps (à un point donné du temps : une date, une année, etc.). Par exemple : la taille d’un échantillon d’une population mesurée à une date précise. Un autre exemple : les notes d’économie à l’examen de juin 2011 de la classe de 1ère année Bachelor ;
- Les séries chronologiques ou temporelles (Time series en anglais) : ce sont des séries dont les valeurs sont prises à différentes dates et concernent le même individu. Par exemple : le PIB suisse de 1990 à 2017 est une série temporelle. En revanche, le PIB des pays membres de l’Union européenne en 2017 est une série transversale.
6. L’économétrie
Au début du XXe siècle, une discipline se développe et donne du poids à la relation entre les sciences économiques et la statistique. Il s’agit de l’économétrie. L’analyse économique se base sur des représentations théoriques analysant les comportements des acteurs économiques ainsi que les relations économiques. Les hypothèses théoriques sont à la base de l’analyse économique. Comment vérifie-t-on la véracité et le réalisme de ces hypothèses ? C’est le rôle de l’économétrie. Il s’agit de la mise en application des méthodes statistiques aux observations des phénomènes économiques. En effet, l’économétrie est un ensemble d’outils et de méthodes statistiques appliqués à l’économie. Elle permet :
- de tester les théories économiques en les confrontant à la réalité (les statistiques),
- d’évaluer les grandeurs et les paramètres représentant les relations économiques, par exemple : évaluer l’impact d’une variable sur autre dans le long terme.
La démarche économétrique consiste à :
- prendre comme point de départ une théorie économique ou une hypothèse,
- traduire cette théorie ou hypothèse en modèle permettant de les confronter aux observations réelles,
- confirmer ou infirmer la validité de la théorie ou de l’hypothèse par les résultats et les tests statistiques, et finalement
- évaluer les valeurs des paramètres et des grandeurs si la théorie n’est pas invalidée dans l’étape précédente.
7. La prévision économique
La prévision économique est un domaine important des sciences économiques. Elle est utile à l’ensemble des acteurs économiques, en particulier les entreprises et l’Etat. Les entreprises ont besoin de voir un peu plus loin pour planifier les investissements futurs et les prises de décisions de gestion. L’Etat a besoin de prévision pour pouvoir mettre en place des politiques économiques appropriées. Les méthodes de prévision sont de deux catégories : les méthodes qualitatives et les méthodes quantitatives.
1. Méthodes quantitatives
Les méthodes quantitatives reposent sur l’extrapolation de la demande dans le temps en utilisant les données des consommations passées. Ci-dessous, nous présentons une liste non exhaustive des méthodes quantitatives :
- Méthode quantitative simple (prise en compte de la demande actuelle plus ou moins un certain pourcentage) ;
- Méthode des moyennes glissantes (moyenne de la demande réelle de (n) périodes antérieures les plus récentes) ;
- Méthode de lissage exponentiel (ou moyenne pondérée par des coefficients exponentiels sur une période) ;
- Méthode de la tendance (projection linéaire, exponentielle, logarithmique ou polynomiale de la tendance passée. A partir des simulations, on choisit celle qui s’adapte le mieux à l’allure de la demande) ;
- Méthode de décomposition (décomposition du résultat des prévisions en tendance, saisonnalité, effets aléatoires) ;
- Méthode de régression et corrélation (utilisation combinée de la droite des moindres carrés et de la corrélation avec une variable de dépendance).
Toutes ces méthodes de prévision ne sont pas exclusives. Elles peuvent être combinées pour diminuer les incertitudes et renforcer la fiabilité des résultats.
2. Méthodes qualitatives
C’est une méthode qui utilise des données subjectives. Les résultats de cette démarche dépendent du jugement personnel, de l’expérience et de l’expertise des personnes fournissant les prévisions. Les opinions des personnes questionnées (vendeurs, consommateurs, cadres, experts, employés, supporters, ...) jouent un rôle fondamental.
Les méthodes qualitatives sont donc des méthodes non quantifiables. Elles sont essentiellement basées sur l’opinion, la comparaison et le jugement. Nous pouvons recenser les méthodes suivantes :
- La méthode de sondage : avec ce procédé nous sondons les opinions des différents acteurs (enquêtes auprès des vendeurs, distributeurs des produits, des consommateurs, etc.) ;
- La méthode de comparaison (ou analogie historique) : prévision par comparaison avec des produits similaires vendus dans le passé ;
- La méthode Delphi : il s’agit de poser des questions à différents experts. Le retour est la réponse à une série de questions par un panel d’experts ;
- Les études de marché (application d’un questionnaire par exemple aux consommateurs éventuels afin d’anticiper sur les changements du marché).
La prévision économique en Suisse
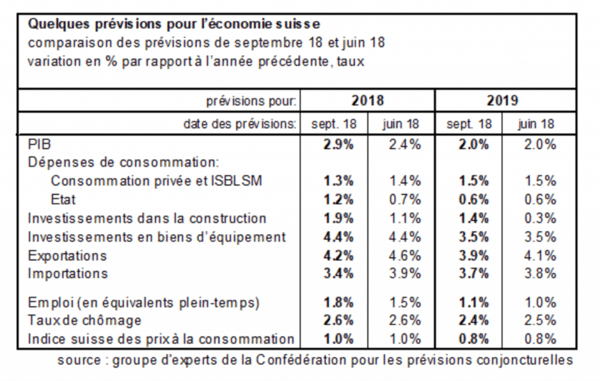
Prévisions conjoncturelles du Groupe d’experts de la Confédération pour l’automne 2018
Le groupe d’experts revoit nettement à la hausse ses prévisions de croissance du PIB pour 2018 pour l’établir à 2,9 % au lieu de 2,4 %. Les bonnes conditions économiques internationales stimulent le commerce extérieur et les entreprises investissent massivement. Une solide croissance du PIB de 2,0 % est toujours attendue pour 2019.
Les risques négatifs prédominent toutefois nettement et menacent la conjoncture internationale. La Suisse connaît actuellement une phase de haute conjoncture. Le PIB a fortement progressé depuis plusieurs trimestres, l’emploi est en hausse et le chômage en baisse. L’industrie a fait montre d’une évolution particulièrement dynamique. Ses capacités de production sont fort utilisées, comme jamais depuis 2011, et les carnets de commandes demeurent bien remplis.
Le secteur des services affiche globalement lui aussi une très bonne marche des affaires. C’est pourquoi le groupe d’experts prévoit, pour l’ensemble de l’année 2018, une progression très marquée du PIB de 2,9 % (prévisions de juin : 2,4 %), même si certains indicateurs suggèrent aujourd’hui un ralentissement de la dynamique.
L’économie d’exportation devrait continuer à stimuler la croissance. Bien que le franc suisse se soit sensiblement apprécié cet été à la suite d’un contexte international plus incertain, la situation du cours du change reste favorable comparativement aux trois dernières années. Par ailleurs, le groupe d’experts s’attend à la poursuite d’une croissance économique robuste au niveau mondial.
En effet, les perspectives aux États-Unis restent bonnes, même si la reprise est installée depuis un moment déjà, et la croissance devrait rester stable en Chine. Cette évolution positive stimulera la demande pour les produits suisses, pour autant que le différend commercial à l’échelle internationale ne s’envenime pas.
Extrait publié par le SECO, 19 septembre 2018.
Tableau : Prévisions pour l’économie Suisse